RAPPORTS ENTRE MÈTRE ET COUDÉE ROYALE : DOIT-ON VRAIMENT CROIRE AU DIEU HASARD ?

Le système métrique a été déterminé en 1795. On a décidé qu’un tour de la Terre vaudrait 40 millions de mètres, Méchain et Delambre en ont mesuré une portion allant de Barcelone à Dunkerque et de cela on a déduit la longueur du mètre telle qu’on la connait. Enfin ça, c’est que l’Histoire nous rapporte… car lorsqu’on met son nez dans cette affaire, on a brutalement envie de devenir Croyant en un nouveau Dieu.

Méchain et Delambre (source : site internet IGN)

Le fait d’avoir déterminé une longueur particulière du mètre a en effet entraîné de surprenantes conséquences.

Un cercle de 1 de diamètre. Son périmètre vaut donc 3,14… si on le divise par 6, alors 1/6 vaut 0,5236
tandis que le reste vaut 2,618, soit le Nombre d’or au carré. On est en proportion.
Si maintenant on décide de tracer ce cercle, avec un diamètre de 1 mètre,
alors le périmètre vaudra 3,14… mètres et le sixième de ce périmètre 0,5236 m

La première conséquence, c’est que la Coudée Royale employée dans la grande pyramide, comme dit plus haut, prend alors pour valeur 1/6 de Pi en mètre, nombre ou plus exactement rapport que les anciens Égyptiens ne sont pas supposés connaître, bien qu’on trouve une valeur approchée de Pi, donnée par l’opération suivante : le demi-périmètre de la pyramide divisé par la hauteur est égal à 3,1428 (au lieu de 3,1416, en se basant sur les dimensions données par l’égyptologie à la pyramide, soit 440 coudées de base sur 280 coudées de hauteur).

C’est le modèle de proportion de la grande pyramide, qui indépendamment des mesures qui seront choisies par la suite pour sa réalisation, donneront toujours ce même résultat pour cette opération.

La coudée = Pi divisé par 6 en mètre : voici donc, notre premier « hasard ».

La Coudée Royale employée dans la grande pyramide se détermine avec exactitude par les mesures de la chambre haute et vaudrait :

0,5235 m selon Gilles Dormion

0,5236 selon Kerisel et Antoniadi

0,5238 selon Newton

soit 52 centimètres 3 millimètres et une variation de quelques dixièmes de millimètres selon les auteurs. On veut bien pinailler, mais il ne faut tout de même pas exagérer, c’est très précis et il est malhonnête de dire qu’on serait « bon an mal an entre 52 et 53 cm » (Jean-Pierre Adam) alors que la coudée employée pour la grande pyramide se déduit avec précision des dimensions de la chambre haute.

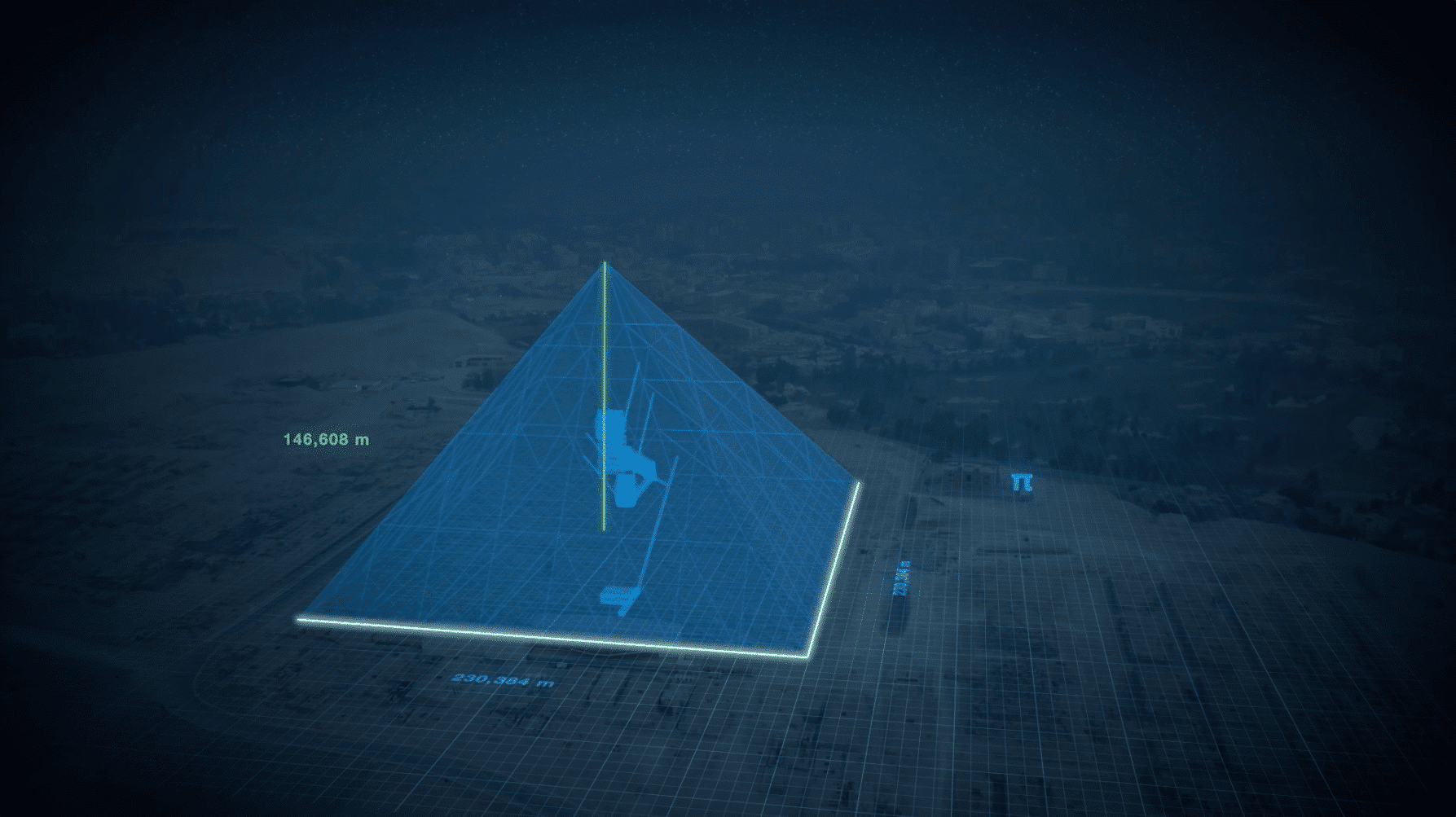
La deuxième conséquence, c’est que les dimensions de la grande pyramide en mètres font que le demi périmètre de la grande pyramide MOINS la hauteur donne 100 x Pi en mètre !

(230,384 x2) — 146,608 = 314,16 m

La chose étonnante étant qu’on se retrouve donc face à une division et d’une soustraction des deux mêmes éléments, le demi-périmètre et la hauteur, qui donnent respectivement pour résultat Pi (à 3,1428…) et 100 x Pi (à 3,1416…) 

Certains rétorquent qu’il ne s’agirait là que d’une conséquence du premier hasard (qui ferait que la coudée vaut 1/6 de Pi en mètre) et que ce enserrait pas intentionnel. Or la grande pyramide aurait pu avoir des mesures physiques différentes, sa base être plus longue ou plus courte de 5 coudées par exemple, et dans ce cas, ses mesures converties en mètres n’auraient pas pu permettre que cette soustraction de la hauteur au demi-périmètre nous donne comme résultat 100 x Pi.

Cela ne découle donc pas du fait que la coudée est égale à 1/6 de Pi, et c’est là un deuxième hasard.

Si votre raison vous souffle que tout cela est impossible, puisque tout le monde sait bien que les Égyptiens ne pouvaient pas connaître le mètre, puisqu’il a été déterminé des millénaires plus tard, c’est parce que vous n’avez pas encore vu BAM et qu’il vous manque des informations pour dépasser cet écueil.

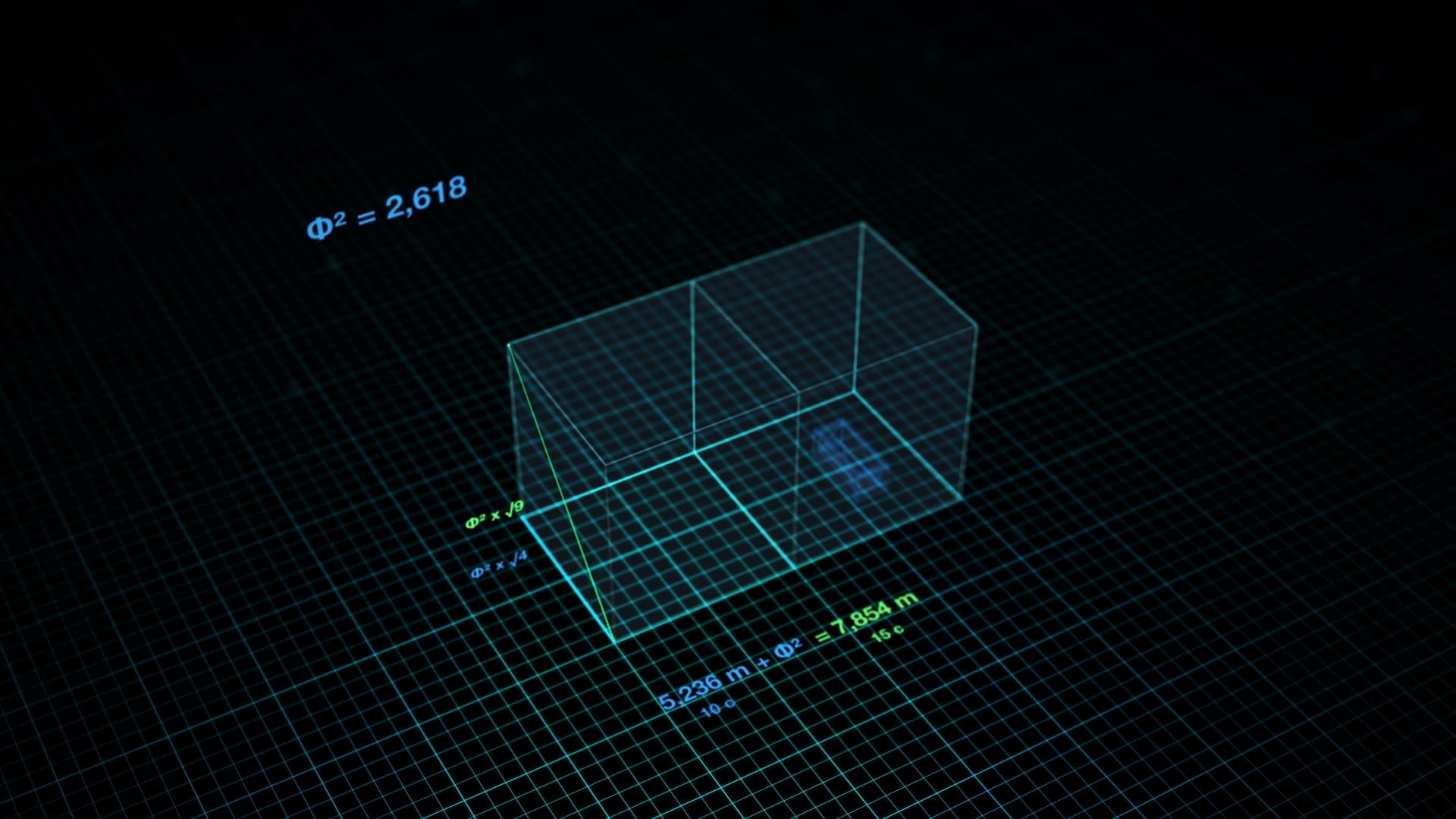
La troisième conséquence, c’est que la chambre haute mesure 10 coudées de large par 20 coudées de long, pour 11,18 coudées de hauteur, ce qui n’est pas très commode pour sa réalisation, car arrondie à 11 ou 12 coudées, cela aurait simplifié le travail s’il ne s’agissait que d’une simple considération esthétique.

Ces dimensions en coudées font que si on les convertit en mètres, le périmètre de ce double carré vaut 10 x Pi en mètre.

Cette chambre est si particulière que, toujours en considérant les dimensions converties en mètre : petit côté + 2,618 m (le Nombre d’or au carré exprimé en mètres) égale la longueur diagonale de la paroi dressée sur le petit côté, etc… un peu compliqué à décrire ce qu’il est plus facile de voir sur ces illustrations de BAM :

Ici encore, ce volume indépendant de la forme de la pyramide qu’est la chambre haute, aurait pu être réalisé physiquement avec d’autres dimensions, qui n’auraient pas pu permettre cette valeur du périmètre égale à 10 x Pi en mètre.

Prosternez vous donc devant ce troisième hasard !

La quatrième conséquence, c’est qu’environ 3500 plus tard – si on se fie à la datation retenue par l’égyptologie – la Coudée Royale médiévale (employée au Moyen Âge) qui appartient à la Quine Royale, une succession de 5 mesures harmonisées par le nombre d’or (qui aurait selon Pascal Warengo, entre autres spécialiste des mesures médiévales, été apportée par la Royauté française Cf BAM), vaut en mètre, 0,5236 mètre (toujours une fois celui-ci déterminé en 1795) tandis que l’empan vaut 20 cm, soit 1/5 de mètre.

Oh mon Dieu, un quatrième hasard ?

Certains pensent que l’illusion statistique expliquerait tout ce qui précède (c’est à dire qu’au milieu de tous les nombres, vous avez statistiquement des chances de trouver tout ce que vous cherchez, ce qui renvoie à l’exemple de la brosse à dents cité dans LRDP par monsieur… Adam), ce qui revient à se prosterner devant le Dieu Hasard, décidément bien inspiré sur ce chantier ainsi que sur ceux des cathédrales.

Il serait temps de le prouver autrement qu’en invoquant le hasard à tout bout de champ, car comme dit également dans LRDP, si le hasard accomplit autant de miracles, mieux vaudrait qu’on l’appelle Dieu. 

Vous comprenez mieux le problème ?

Ne serait-il pas plus simple, plutôt que de s’en remettre chaque fois au hasard en prenant les bâtisseurs de cette grande pyramide pour de chanceux crédules, d’envisager rationnellement que nous ne serions pas les inventeurs du mètre, que celui nous aurait été légué, ce qui impliquerait, rien de moins, que les dimensions de la Terre auraient été connues dans un passé lointain ?

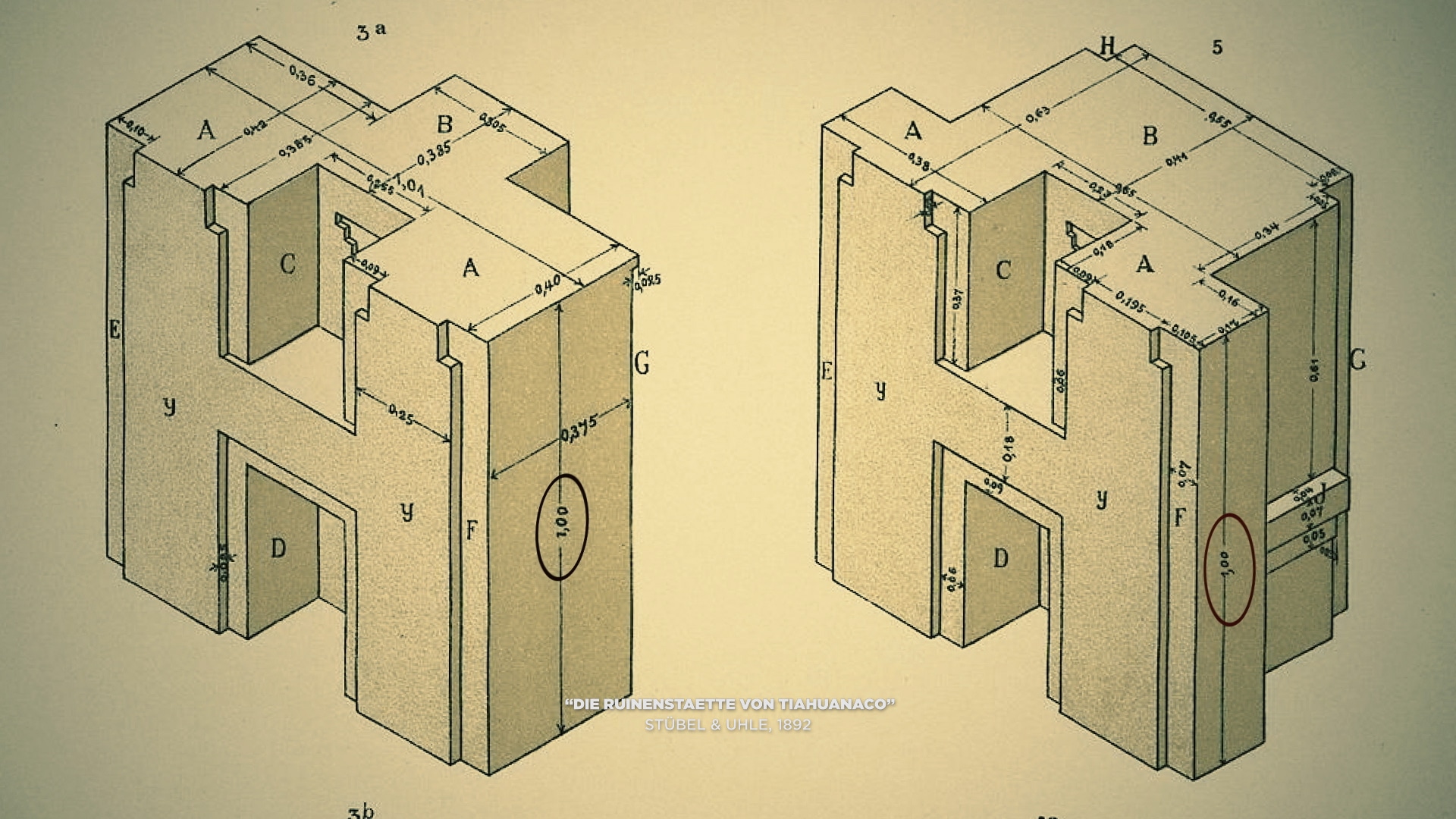
Et accessoirement, cela éviterait d’attribuer une fois de plus au Dieu Hasard le fait que les dimensions de ces blocs en H, aux formes plus que complexes et taillés dans une roche dure comme l’acier trempée, découverts sur le site de Puma Punku en Bolivie mesurent 1 m de hauteur pour 1 m de largeur (avec au dos une croix qui mesure 30 cm de largeur et un renfoncement de 22 cm, ce qui se répète sur plusieurs blocs avec un écart maximal de 1 mm, cf une fois de plus BAM) :

Que le diamètre de la Terre, une fois la valeur de 40 millions de mètres attribuée à sa circonférence polaire, soit très très proche de 10 000 x la racine carrée du Nombre d’or (là ça se complique car au fond de la réflexion, on en vient à envisager que le mètre puisse ne pas être si aléatoire que ça, ce qui nécessite un peu de recul si vous découvrez le sujet) :

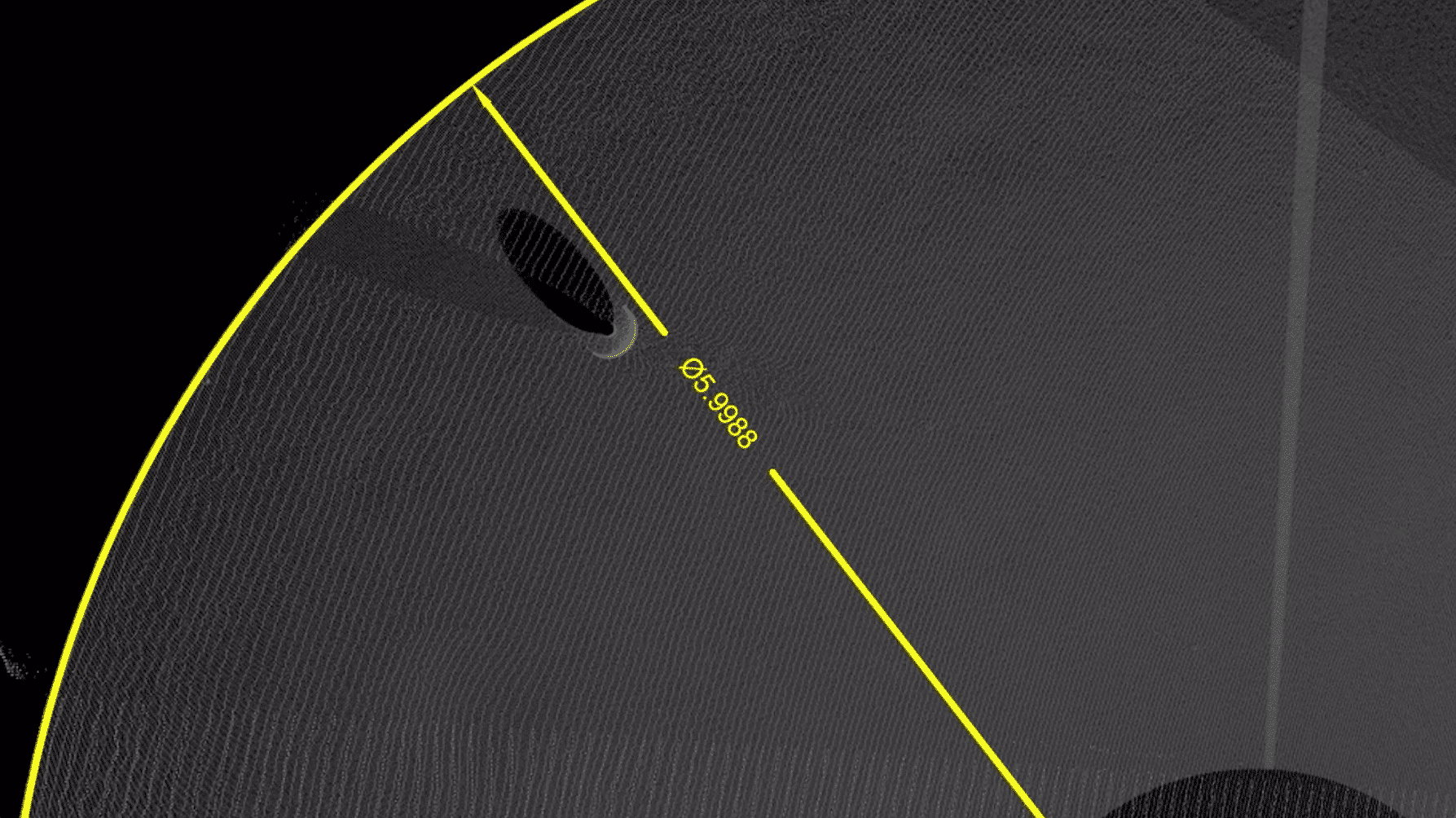
Ou encore que dans la grotte Sudama à Barabar, le dôme composé d’un cône tronqué, sur lequel repose une coupole en exacte portion de sphère, présente d’étonnantes caractéristiques : le disque au sol mesurant 6 mètres de diamètre (à 1 mm près) la portion de sphère pour rayon 3 m (à 5 cm près) et son centre se trouve à 1 m au dessus du sol (à 1 cm près) :

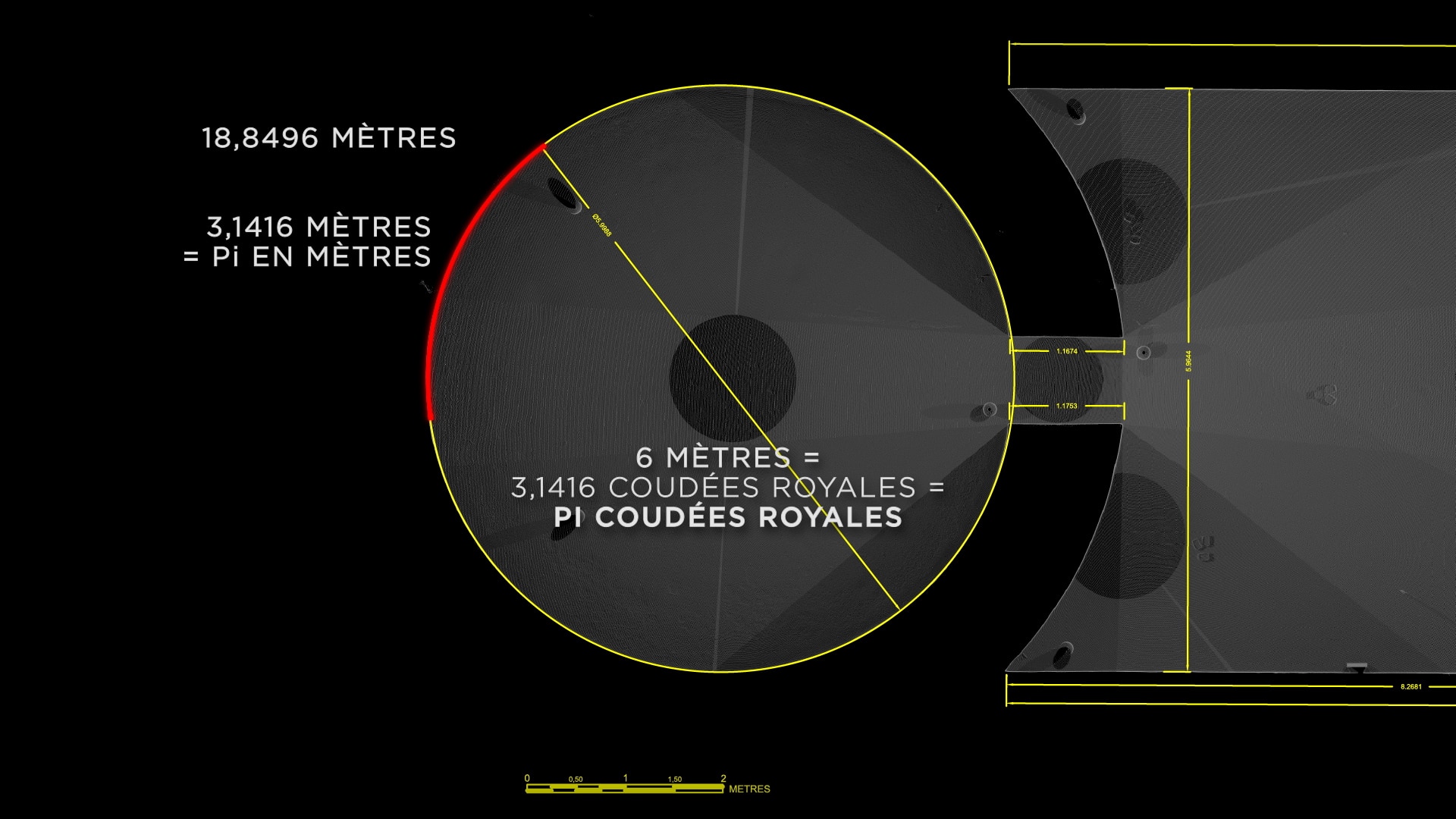
Une erreur s’est glissée dans cette figure : 6 mètres de diamètre ne valent pas Pi en coudées royales, toutes mes excuses
en revanche, 1/6 de ce cercle vaut bien 3,14 mètres, soit Pi en mètres ! On peut toujours rétorquer qu’il ne s’agit que d’un hasard,
mais alors on peut s’étonner que dans une salle aussi précise dans ses dimensions, on ait choisi pour ce dôme –
ainsi que pour la largeur de la salle – des dimensions étonnamment composées de nombres entiers en mètre, ce qu’on retrouve également dans une autre grotte. Nous allons utiliser les scans 3D pour faire des relevés métrologiques précis et ainsi déterminer les dimensions exactes,
car celles présentées ici – confirmant celles sur place au télémètre pour le diamètre du disque – ont été rapidement extraites :
précises, mais une seule mesure pour chaque, alors qu’il en faut plusieurs autour d’un point pour valider.

On peut à loisir attribuer tout ça au hasard et dire que ce sont des foutaises… c’est plus commode et ça évite de réfléchir.

Mais face à la complexité de réalisation et à l’exigence de précision, des blocs d’andésite de Puma Punku (précision qui se répète de l’un à l’autre), à la grande pyramide de Gizeh et les blocs massifs de granite qui composent sa chambre haute (qu’ils sont allés chercher à 900 km du site), en passant par ces étonnantes grottes de Barabar, les plus extraordinaires au monde, on peut aussi se demander si quelque chose ne nous aurait pas échappé dans la compréhension des mystères de notre passé… un quelque chose qui rend la chose incroyable, au vrai sens du terme, mais pourtant on ne peut plus rationnelle, quand on raisonne sans oeillères, dues aux a priori et aux préjugés conditionnés par le carcan historique.

Et alors, qu’est-ce qu’on en a à faire de ces histoires de mètres et de coudées ?, vous demanderez-vous peut-être, ou encore, qu’est-ce que ça va changer à mon quotidien ?

Peut-être qu’en vous retrouvant face à ces édifices majestueux et durables, réalisés par des ouvriers hautement qualifiés dont les oeuvres témoignent d’un immense savoir, d’une maîtrise absolue de la pierre et d’une recherche d’excellence, vous aurez certainement envie de vous questionner et de questionner le monde : c’est là le plus important, dans la drôle de période de l’Histoire que nous traversons… que bâtissons-nous pour la postérité ? N’y a-t-il plus rien qui nous rende fiers ?

On ne l’aperçoit pas tout de suite, car il faut un peu de temps pour voir le tableau d’ensemble, mais en réalité, si on découvrait que nos ancêtres étaient bien plus avancés que ce qu’on pense généralement, que le sens du progrès n’était pas aussi linéaire qu’on le croit, alors je suis convaincu qu’il y aurait nécessairement des choses bénéfiques à en retirer pour notre civilisation et que cela pourrait changer notre avenir.

Bon voyage !

Ici un excellent article de Quentin Leplat qui nous livre son travail sur le mètre : bravo à lui de continuer dans ses recherches, envers et contre tout.

Tout ça passe vite dans BAM, mais a le mérite de s’intégrer dans une réflexion plus globale.
Si vous ne l’avez pas encore vu, il est en streaming ici.

Et si vous souhaitez revoir tout ça en détail chez vous, à votre rythme, alors BAM existe aussi en livre.